PROBABILITY DISTRIBUTIONS, EXPECTED VALUES AND MOMENTS
In contrast to deterministic quantities that are described by a particular numerical value, random variables can only be completely described by their probability distributions. These mathematical functions have a number of particular characteristics that are presented in the following descriptions. Here we focus on continuous random variables but these ideas can be easily generalized to discrete random variables as well.
(QUESTION: should I include discrete distributions?)
Univariate probability distributions
A continuous random variable is completely described by the probability density function (pdf), given as f(x). The pdf has certain specified properties:
![]() , for all values of x, and
, for all values of x, and
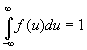
The random variable need not be defined on the entire real line but might only be defined for positive values as for many variables of interest in environmental problems. (add a figure to show the normal and one other distribution that is only defined on positive values) In that case, the integration proceeds from the lower limit of the variable, often zero, to the upper limit. There are many functions that satisfy these minimal conditions and are therefore pdf's. One of the major problem associated with statistics is to determine the appropriate pdf to describe a particular random variable. (add and example illustrating these properties, e.g. uniform and/or exponential distributions)
Associated with the pdf is the cumulative distribution function (cdf), defined as:
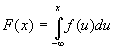
Again, if the variable has a lower limit, the integration begins at the lower limit. As indicated by the name, the cdf is a function of the particular value, x. The value of the cdf gives the probability that the random variable X, is less than or equal to a particular numerical value, x. This can be mathematically stated as:
![]()
The situation that X < x is a particular event and the probability is related to that event. The cdf can be geometrically interpreted as the area under the pdf from the lower limit of X to the particular numerical value, x. (add a figure to illustrate this concept and an example for calculating the cdf, e.g. the exponential distribution)
The cdf is the basis for the calculation of probabilities. For example, consider the event described by the inequality: x1 < X < x2. The probability associated with this event is given by:
![]()
This relationship can be interpreted by visualizing the area under the pdf. (add a figure to illustrate this concept)
In summary, if the pdf of a random variable is known (or can be determined) then the probability of events associated with that random variable can be calculated from the cdf. Since all pdf’s are parametric functions, process of selecting and fitting a distribution for a process involves selecting a distribution with the appropriate shape and selecting the correct parameter values.
Multivariate probability distributions
Analogous to the univariate situation, when there is more than one random variable, we can have a joint pdf that completely describes behavior of all of the random variables together. The most common situation is the case of two random variables where the joint pdf is usually written as f(x,y) if x and y are the random variables. The joint pdf has the same properties as the univariate pdf; that is the function must be non-negative and integrate to 1.0 over the domain of the random variables. Random variables are said to be stochastically independent if their joint pdf is simply the product of their respective univariate pdf's (also called their marginal distributions) as:
![]()
The distribution of a random variable given conditions on a related random variable is called the conditional distribution and is written as f(x|y). The conditional pdf is computed from the joint and marginal pdf's as:
![]()
Based on the definition of independence, if x and y are independent the conditional distribution is the marginal distribution. The conditional distribution is of particular significance in regression analysis.
Expected value
A mathematical relationship that has widespread applicability in probability and statistics is the expected value or expectation of a random variable of function of a random variable. The expected value is defined as:
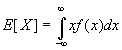
The random variable, X, can be replaced by any function of a random variable to determine the expected value of that function. For example, the expected value of the function g(X) where X is a random variable is given by:
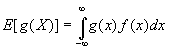
The expected value notation is widely used in discussions related to random variables. There are a number of additional properties of expected value that follow directly from the definition and apply when the function, g(x), is linear. In general, they are related to the expected value of functions of random variables. Some useful relations are:
![]() , where c is a constant
, where c is a constant
![]() , where c is a constant
, where c is a constant
![]() , where the ci’s are constant terms
, where the ci’s are constant terms
Moments
An important and useful description of the nature of a random variable can also be obtained through the use of its moments. The moments can often be used as an indication of the shape of the pdf and thus the distribution of the random variable. In general, we will use the symbol µ'r to indicate the rth moment of a random variable, X, defined as:
![]()
Notice that the rth moment is the expected value of xr. The first moment, called the mean, is used very frequently in the description of a random variable. In fact it is used so frequently that it is normally described by the symbol µ. Mathematically, the mean is expressed as:
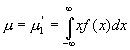
The mean is the geometric center (centroid) of the pdf and is a measure of central tendency for the random variable. The mean , therefore, represents the value of the random variable at the centroid of the pdf.
It is common to express the higher order moments of a random variable in a slightly different manner. Normally, the central moments, or moments of the deviation of the random variable from the mean, are used. The central moments are usually given the symbol ![]() and are defined as:
and are defined as:
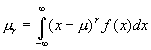
There are higher order moments that are commonly used in the description of random variables. The most common and useful are the second and third central moments. The second central moment, called the variance, is usually given the symbol ![]() and is defined as:
and is defined as:
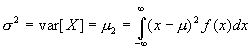
Being the squared deviation of the random variable from its mean value, the variance is always positive and is a measure of the dispersion or spread of the distribution. The square root of the variance is called the standard deviation , ![]() ,and is more useful in describing the nature of the distribution since it has the same units as the random variable. The standard deviation is given by:
,and is more useful in describing the nature of the distribution since it has the same units as the random variable. The standard deviation is given by:
![]()
The third central moment, ![]() , is called the skewness and is a measure of the symmetry of the pdf. The skewness can have a positive value in which case the distribution is said to be positively skewed with a few values much larger than the mean and therefore a long tail to the right. A negatively skewed distribution has a longer tail to the left. A symmetrical distribution has a skewness of zero.
, is called the skewness and is a measure of the symmetry of the pdf. The skewness can have a positive value in which case the distribution is said to be positively skewed with a few values much larger than the mean and therefore a long tail to the right. A negatively skewed distribution has a longer tail to the left. A symmetrical distribution has a skewness of zero.
Finally, there are some combinations of the moments and central moments that are also commonly used. The coefficient of variation is the ratio of the standard deviation to the mean and is given by:
![]()
The coefficient of skewness is the ratio of the skewness to the standard deviation raised to the third power:
![]()
The coefficient of skewness has more convenient units than does the skewness and often ranges from -3.0 to 3.0 for data from natural systems. Again, a symmetrical distribution has a coefficient of skewness of zero. A positive value of Cs often indicates that the pdf exhibits a concentration of mass toward the left and a long tail to the right whereas a negative value generally indicates the opposite.
There are similarly useful moments for bivariate distributions that can be used to describe the nature of the relationship between two random variables. The most commonly used and potentially the most important of these is called the covariance between two random variables, X and Y, and is given by:
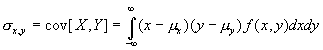
Related to the covariance is the correlation coefficient, a measure of the linear association between two random variables, X and Y. The correlation coefficient is given by:
![]()
The correlation coefficient ranges between 1.0 and -1.0. The correlation coefficient can be used as an indicator of the degree of association between two random variables. A value of 1.0 (or -1.0) indicates a perfect linear relationship between the two variables. A value of 0.0 indicates no linear association. Random variables that are stochastically independent have a correlation coefficient of 0.0.
One adaptation of the correlation coefficient is its use to describe random variables that represent a time series. The correlation coefficient between values of the time series separated by a specific time lag is called the autocorrelation coefficient. The autocorrelation coefficient can be computed for successive lag times and be represented as a function of the lag time. This is called the autocorrelation function (acf) and, for a time series, ![]() , is given by:
, is given by:
![]()
The acf is usually a decreasing function of lag time indicating a decreasing association between values of the variable as the time difference increases. In a time series where there is no dependence between successive values, that is for an independent, identicallydistributed random variable, the acf is zero.
Relationship of moments to expected values
Since moments are simply special cases of the expected value, there is a relationship between the various moments and expected values of the random variables. The mean is simply the expected value of the random variable, that is:
![]()
Based on the definition of the variance and the expected value, the variance can be written in terms of expected values by:
![]()
Higher order moments can be written in a similar fashion.
The covariance can also be written in terms of expected values as:
![]()
It is common to have a need to compute the moments of a sum of random variables. Following from the definition of the expected value and the moments:
![]()
This relationship indicates that the mean of a sum is the sum of the means. However, in general, the variance is not as simply expressed:
![]()
If the random variables Xi, i = 1, 2 ....n, are independent so that the covariance is zero except where i = j, the expression for the variance reduces to:
![]()
So in this special case, the variance of the sum is equal to the sum of the variances.
Some other properties of random variables and distributions
There are at least two other properties of random variables and pdf's that are of interest and both relate to the central tendency. The median is defined as the value that the random variable exceeds with a probability of 0.5. Mathematically, the median is given by:
![]()
The mode is the maximum value of the probability density function. For symmetrical distributions, the mean, median and mode have the same value.